 |
|
 |
|

|
MATEMATIKA adalah suatu ilmu yang memang banyak digemari oleh orang-orang yang cenderung menyukai angka. Tetapi tidak sedikit juga mereka yang kesulitan dalam menyelesaikannya.
Padahal sejatinya, asalkan kita terbiasa, cermat dan teliti pasti akan lebih mudah memahaminya. Dan untuk kali ini, kita akan mengenal apa itu himpunan? Dan apa saja macam-macam himpunan yang bisa kita pelajari.
Pengertian Himpunan: Himpunan merupakan suatu kumpulan benda-benda atau objek-objek yang didefinisikan dengan jelas. Benda dan objek yang termasuk dalam himpunan disebut dengan anggota atau elemen himpunan tersebut.
Sebagai contoh, kumpulan negara ASEAN, kumpulan buku-buku pelajaran, kumpulan bilangan bulat, kumpulan hewan berkaki empat, dan sebagainya.
Himpunan biasanya dilambangkan dengan huruf kapital seperti A, B, C ataupun yang lainnya yang dituliskan dalam tanda kurung kurawal, seperti: A = {Himpunan buah-buahan berwarna kuning}. B = {Merah, kuning, hijau}. C = {...,-3,-2,-1,0,1,2,3...}.
Penyajian Himpunan: Himpunan bisa disajikan dengan beberapa cara, berikut beberapa penyajian himpunan:
-1. Menyebutkan Syarat Anggota. Ex: A = Himpunan empat bilangan asli genap pertama. B = Himpunan bilangan cacah ganjil. C = Himpunan nama-nama buah yang diawali dengan huruf S.
-2. Menyebutkan/Mendaftarkan anggota-anggotanya/Tabulasi/Eliminasi. Ex: A = {2,4,6,8}. B = {0,1,3,5,7,9...}. C = {Semangka, Sirsak, Srikaya, Salak}.
-3. Notasi Pembentuk Himpunan. Ex: A = {X | X < 9, X elemen bilangan asli genap}. B = {X | X elemen bilangan cacah ganjil}. C = {X | X elemen nama buah berawalan S}.
-4. Diagaram Ven.
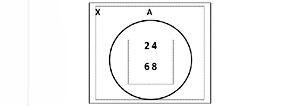
Contoh: Tuliskan dengan notasi pembentuk himpunan untuk bilangan asli yang... -a. Kurang dari 10. -b. Lebih dari 1 dan kurang dari sama dengan 4. Jawabannya: -a. {X | X < 10, elemen bilangan asli}. -b. {X | 1 < X ≥ 4, X elemen bilangan asli}.
Macam-macam Himpunan: Ada beberapa macam-macam himpunan yang bisa kita pelajari, antara lain:
Himpunan Kosong: Himpunan kosong merupakan himpunan yang tidak mempunyai elemen atau anggota. Biasanya himpunan ini sering disebut himpunan null yang disimbolkan dengan tanda “{}”.
Notasi: ∅ dan {}. Ex: -1. A = Himpunan nama hari yang diawali dengan huruf B. -2. B = Himpunan bilangan ganjil yang habis dibagi dua.
Himpunan Bagian: Himpunan A dapat dikatakan sebagai himpunan bagian (subset) dari himpunan B apabila semua anggota A ada di dalam himpunan B. Dan himpunan B merupakan super himpunan (superset) dari himpunan A karena semua elemen A juga adalah elemen B.
Notasi: ⊂ untuk subset dan ⊃ untuk superset. Ex: -A = {1,2,3,4,5,6}. -B = {1,2,3,4}. Jawabannya: Seluruh anggota himpunan B ada dalam himpunan A, maka B ⊂ A dan A ⊃ B.
Himpunan Yang Sama: Disebut sebagai himpunan yang sama apabila himpunan A dan himpunan B memiliki anggota tang sama. Maksudnya A sama dengan B apabila A merupakan himpunan bagian dari B dan B merupakan himpunan bagian dari A.
Notasi: A = B ↔ A ⊂ B dan B ⊂ A. Ex: -A = {3,6,8,5,6}. -B = {3,5,6,8}. Maka: A ⊂ B dan B ⊂ A.
Himpunan Yang Ekivalen: Himpunan ekivalen yaitu apabila himpunan A dan himpunan B memiliki jumlah anggota yang sama.
Notasi: A ~B ↔ n (A) = n (B). Ex: -A = {6,7,8,9,10}. -B = {a,b,c,d,e}. Banyaknya anggota himpunan A, n(A)=5. Banyaknya anggota himpunan B, n(B)=5. Maka, himpunan A ekuivalen dengan himpunan B.
Catatan: jumlahnya atau banyaknya elemen himpunan harus sama walaupun beda jenisnya.
Himpunan Saling Lepas: Himpunan saling lepas (disjoint) apabila himpunan A dan himpunan B tidak memiliki elemen yang sama.
Notasi: A // B. Ex: -A = {7,8,9}. -B = {2,3,4}. Maka, himpunan A saling lepas dengan himpunan B atau A // B.
Himpunan Kuasa: Power set atau himpunan kuasa misal dari himpunan A adalah suatu himpunan yang seluruh anggotanya merupakan himpunan bagian dari A, termasuk himpunan kosong dan himpunan A itu sendiri.
Notasi : P (A) atau 2a. Ex: -A = {1,2}. -P(A) : 2a. -2² = 4. = {∅, (1), (2), (1,2)
Itulah pengertian dan beberapa macam himpunan yang bisa kita ketahui, pahami dan pelajari. Tidak ada yang sulit selagi kita yakin dengan diri kita sendiri dan optimis dalam menyelesaikannya.
Yakin dan terus yakin bahwa kita bisa, bahkan jauh lebih bisa dari pada yang lain. Tetap semangat untuk belajar, jangan pernah menyerah, teruslah pelajari apa yang memang kita belum pahami.
